§3.1
中值定理
一、罗尔定理
若![]() 在闭区间
在闭区间![]() 上连续,开区间
上连续,开区间![]() 内可导,且
内可导,且![]() ,则至少存在一点
,则至少存在一点![]() ,使
,使![]() 。
。
在证明罗尔定理之前,我们先来描述一下它的几何意义。
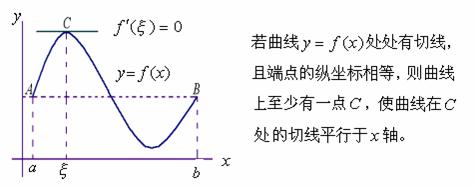
为了使同学们更直观地看到这一点,我们在计算机上做一个动画实验:
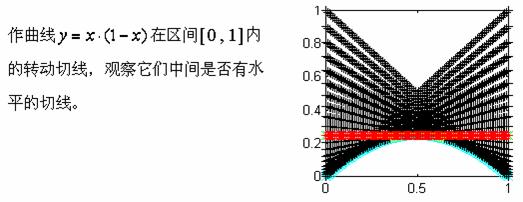
【定理证明】
![]() 在
在![]() 上连续,据闭区间上连续函数的最大值和最小值定理,
上连续,据闭区间上连续函数的最大值和最小值定理,![]() 在
在![]() 上取得最大值
上取得最大值![]() 和最小值
和最小值![]() , 这样只有两种可能情形:
, 这样只有两种可能情形:
(1)、![]() 。 这时
。 这时 ![]()
![]()
![]() , 有
, 有 ![]() 。
。
(2)、![]()
因![]() , 所以
, 所以 ![]() 和
和 ![]() 中至少有一个不等于
中至少有一个不等于 ![]() ,
,
不妨设 ![]() ,
, ![]() ,使
,使 ![]()
下面证![]() 在点
在点![]() 处的导数等于零,即
处的导数等于零,即 ![]() 。
。
因![]() 存在,故极限
存在,故极限![]() 存在,故其左、右极限均存在且都等于
存在,故其左、右极限均存在且都等于![]() 。
。
因 ![]() ,当
,当 ![]() 时,有
时,有
![]()
从而 ![]()
当 ![]() 时,有
时,有
![]()
从而 ![]()
故 ![]()
罗尔定理的三个条件缺一不可,否则结论不真。试看下例:
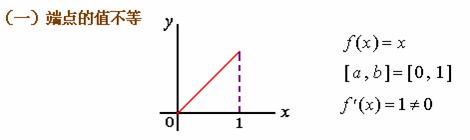
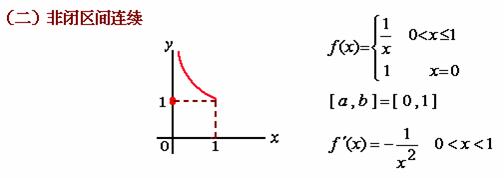

二、拉格朗日中值定理
去掉罗尔定理中相当特殊的条件 ![]() ,仍保留其余两个条件,可得到微分学中十分重要的拉格朗日中值定理。
,仍保留其余两个条件,可得到微分学中十分重要的拉格朗日中值定理。
【拉格朗日中值定理】 若![]() 在闭区间
在闭区间![]() 上连续,在开区间
上连续,在开区间![]() 内可导,则至少存在一点
内可导,则至少存在一点![]() ,使得
,使得
![]() (1)
(1)
在证明之前,我们先看一下定理的几何意义。
![]() 是弦
是弦![]() 的斜率,
的斜率,![]() 为曲线在点
为曲线在点![]() 处的切线斜率。在曲线
处的切线斜率。在曲线![]() 上至少有一点
上至少有一点![]() ,使曲线在
,使曲线在![]() 点处的切线平行于弦
点处的切线平行于弦![]() 。
。
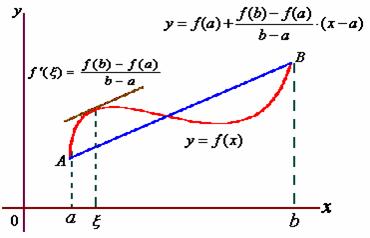
由于拉氏中值定理与罗尔定理十分相似,我们设法构造一个满足罗尔定理三个条件的辅助函数![]() ,利用它完成拉氏中值定理的证明。很自然地,取弧AB与弦AB所代表的函数之差就行了。
,利用它完成拉氏中值定理的证明。很自然地,取弧AB与弦AB所代表的函数之差就行了。
【证明】作辅助函数
![]()
![]() 在
在![]() 上连续,在
上连续,在![]() 可导,且
可导,且![]() ,由罗尔定理,至少存在一点
,由罗尔定理,至少存在一点 ![]() ,使
,使 ![]() ,即
,即
![]()
亦即 ![]() 。
。
把拉氏中值定理的证明思想移植到具体函数
![]()
上,我们编写了一个matlab程序gs0302.m,可较直观地验证上述证明思想的正确性。
拉氏中值定理是微分学中最基本的一个定理,有广泛的应用。我们对它特别给出如下重要注解。
1、当![]() 时式子(1)仍然成立。
时式子(1)仍然成立。
2、设![]() ,
,![]() (
( ![]() 或
或 ![]() ),在区间
),在区间![]() (
( ![]() ) 或
) 或 ![]() (
( ![]() )上使用拉氏中值定理,我们有
)上使用拉氏中值定理,我们有 ![]()
由于![]() 可正可负,因此,无法确定是区间
可正可负,因此,无法确定是区间![]() ,还是区间
,还是区间![]() ,因此,我们只能讲“
,因此,我们只能讲“![]() 在
在 ![]() 与
与 ![]() 之间”。
之间”。
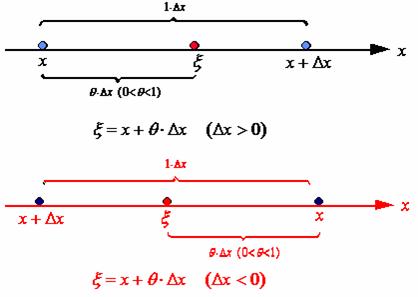
如下图所示,![]() 可表示成为:
可表示成为:
![]() (2)
(2)
更一般地,在![]() 或
或![]() 上使用拉氏中值定理有:
上使用拉氏中值定理有:
![]() (3)
(3)
3、![]() 在开区间
在开区间![]() 内的导数恒为零
内的导数恒为零 ![]()
![]() 在
在![]() 内恒为常数。
内恒为常数。
【证明】
充分性(![]() )设
)设![]() ,显然
,显然 ![]() 。
。
必要性(![]() )
)![]() ,
,![]()
由拉氏中值定理有
![]()
由 ![]() ,得
,得 ![]()
故![]() 在
在![]() 内的任意两点的函数值均相等,即
内的任意两点的函数值均相等,即
![]() 。
。
三、柯西中值定理
若函数![]() 、
、![]() 满足下述三个条件:
满足下述三个条件:
(1)、![]() 、
、![]() 在
在 ![]() 连续;
连续;
(2)、![]() 、
、![]() 在
在 ![]() 可导;
可导;
(3)、![]() ,
,
则至少存在一点 ![]() , 使得
, 使得
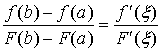 (4)
(4)
柯西中值定理的几何意义也十分明显,考虑由参数方程所表示的曲线
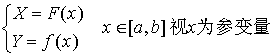

曲线上点 ![]() 处的切线斜率为
处的切线斜率为 ![]()
弦![]() 的斜率为
的斜率为 ![]()
假定点![]() 对应于参数
对应于参数![]() ,那未曲线
,那未曲线![]() 点处切线平行于弦
点处切线平行于弦![]() ,
,
于是 ![]()
【证明】首先注意到![]() ,这是由于
,这是由于
![]()
其中![]() ,根据假定
,根据假定![]() ,又
,又![]() ,所以
,所以
![]()
作辅助函数
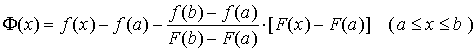
显然,适合罗尔定理的条件:
![]() ;
;
![]() 在
在![]() 上连续;
上连续;
![]() 在
在![]() 上可导, 且
上可导, 且
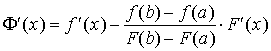
根据罗尔定理,![]() ,
,![]() ,即
,即
![]()
故 ![]()
对这三个中值定理,我们给出几点注解:

2、后两个中值定理的证法: 构造辅助函数,将之化归为罗尔定理的情形。这种考虑问题的方式,在数学与计算机编程上十分有用,称为“归一法”。
何为归一法呢? 下面的一段轶文可生动地说明其涵义。
人物:面试教师, 参试者甲(作家), 参试者乙(数学家)。
面试教师:
烧一壶开水的方法可简述为:
(1)给壶装满水![]() (2)将壶放到煤气灶上
(2)将壶放到煤气灶上![]() (3)煤气灶点火
(3)煤气灶点火![]() (4)待水沸腾,将壶拿下。
(4)待水沸腾,将壶拿下。
若已知第二步已完成,该如何进行才能烧壶开水了? 请二位分别回答。
作 家:
给煤气灶点火,待水烧开后,将壶拿下。
数学家:
将壶中水倒掉,把问题化归为情形(1)就行了。
归一法:
若问题A的结构与解决步骤清楚了,求解问题B时,只需设法化B为A即可。
四、中值定理运用举例
【例1】试证:
当![]() 时, 有不等式
时, 有不等式 ![]() 。
。
【证明】考虑辅助函数 ![]()
由拉氏中值定理有
![]()
即 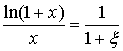
而 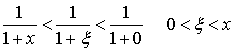
故 ![]()
![]()
【例2】对函数![]() 、
、![]() 在
在![]() 上验证柯西中值定理的正确性。
上验证柯西中值定理的正确性。
【解】显然在上满足柯西中值定理的三个条件:
![]() 、
、![]() 在
在![]() 上连续,在
上连续,在![]() 上可导,且
上可导,且
![]()
欲在![]() 上找到一点
上找到一点 ![]() 使下式成立
使下式成立
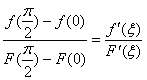 即
即 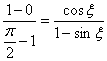
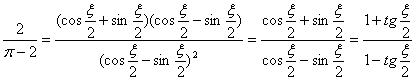
![]() ,
,
![]()
![]() ,
,
![]() ,
, ![]()
只需取 ![]() ,显然
,显然 ![]()
这就验证了柯西中值定理的正确性。